Analyzing Hidden Themes in Retracted Biomedical Literature
Posted on Sun 12 May 2019 in Data Science
In my previous blog post, I discussed various players involved in retractions in biomedical and life science literature. One question that intrigued me and was left unanswered was — what are the research topics/themes that are present in these retracted publications? I attempt to answer this question in this blog post using topic modeling.
Topic modeling is finding, organizing and understanding textual information from a corpus or collection of documents. It is an unsupervised learning approach where the topic model learns the topics in unlabeled documents. It is based on assumptions that each topic is made up of groups of words and each document is a collection of topics. Thus, latent or hidden topics in a corpus can be found out through the collection of words that frequently co-occur.
There are many topic modeling techniques available. Here, I have used one of the most popular techniques, Latent Dirichlet Allocation (LDA)1.
Latent Dirichlet Allocation
LDA is a generative probabilistic model of a collection of documents. It is based on Dirichlet distribution, which is a distribution over multinomial distributions, and assumes that documents are a probability distribution over latent topics and topics are probability distribution over words. LDA backtracks and uncovers different topics that make the corpus and how much of each topic is present in a document.
Mathematically, this generative process can be explained as follows:
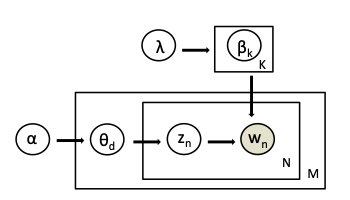 Such a diagram is referred to as a Plate notation. From a Dirichlet distribution with parameter $\lambda$ we obtain a distribution over words for a topic $k \in 1..K$ and this is represented as $\beta_k$. Here, each topic is an $N$-dimensional vector ($N$ is the size of vocabulary) that has probability for each word in topic $k$ according to the distribution $\beta_k$. From a second Dirichlet distribution with parameter $\alpha$ we draw a distribution over topics for every document $d \in 1..M$ and this is represented as $\theta_d$. Thus, for each document, we have a $K$-dimensional vector that has probability for each topic ($K$ is the number of topics) according to this distribution over topics. For each word position $n \in 1..N$ in the document we draw a topic assignement $z_n$ from $\theta$. We then use $\beta$ corresponding to the topic assignment $\beta_{z_n}$ to generate the word. As LDA is aware of the words, it intends to find $z$, $\beta$ and $\theta$.
Such a diagram is referred to as a Plate notation. From a Dirichlet distribution with parameter $\lambda$ we obtain a distribution over words for a topic $k \in 1..K$ and this is represented as $\beta_k$. Here, each topic is an $N$-dimensional vector ($N$ is the size of vocabulary) that has probability for each word in topic $k$ according to the distribution $\beta_k$. From a second Dirichlet distribution with parameter $\alpha$ we draw a distribution over topics for every document $d \in 1..M$ and this is represented as $\theta_d$. Thus, for each document, we have a $K$-dimensional vector that has probability for each topic ($K$ is the number of topics) according to this distribution over topics. For each word position $n \in 1..N$ in the document we draw a topic assignement $z_n$ from $\theta$. We then use $\beta$ corresponding to the topic assignment $\beta_{z_n}$ to generate the word. As LDA is aware of the words, it intends to find $z$, $\beta$ and $\theta$.
In brief, LDA works as follows: First we assign the number of topics $K$ that we expect in the corpus. Then LDA randomly assigns topic to each word in each document. Next, it goes to each word in the corpus and checks how many times that specific topic occurs in a document and how many times that specific word occurs in the assigned topic. Based on the results it assigns a new topic to that specific word and this iteration keeps going until topics make sense. In the end, it is up to the user to interpret the topic.
This blog post will describe the following steps to extract latent topics from my corpus of retrated literature.
- Data preprocessing
- Building an LDA model
- Visualization
As mentioned in my previous blog post, the data was obtained from Pubmed and contains 6485 retracted publications. For the current analysis I have used only the abstracts from these publications. Keywords can be used to determine the theme of any abstract but in the available dataset 84% of the abstracts had no keywords and this motivated me to extract topics from the abstracts.
Data Preprocessing:
This step involves data cleaning and is crucial in any text mining task. I have subdivided this into 3 steps:
i. Lemmatization
This part involves part-of-speech (POS) tagging to filter words that are either noun, proper noun, or adjective. I ignored other parts of speech such as verbs and adverbs as they appeared to be not important to my current task. The resulting words were then lemmatized, which means only the root form of the word was kept. I used the awesome Python library, spaCy, for doing this processing.
# load spacy and return english language object
nlp=spacy.load('en_core_web_sm')
def lemmatization(doc, allowed_pos=['NOUN','ADJ','PROPN']):
``` filtering allowed POS tags and lemmatizing them```
retracted_corpus=[]
for text in doc:
doc_new = nlp(text)
retracted_abstract=[]
for token in doc_new:
if token.pos_ in allowed_pos:
retracted_abstract.append(token.lemma_)
retracted_corpus.append(retracted_abstract)
return retracted_corpus
abstract_lemmatized = lemmatization(doc,allowed_pos=['NOUN','ADJ','PROPN'])
These are scientific documents and sometimes breaking sentences by space alone is not optimal (e.g., a formula or equation may use other characters such as $=$ or $+$). Therefore in an additional step I used a different text splitting implementation using some functionality from NLTK, another Python library for natural language processing (NLP).
from nltk.tokenize import RegexpTokenizer
# tokenizer that splits only in the selected symbols or space
tokenizer=RegexpTokenizer('\s+|[<>=()-/]|[±°å]',gaps=True)
def remove_punctuation(text):
updated_abstract=[]
for doc in text:
sent=' '.join(doc)
updated_abstract.append(tokenizer.tokenize(sent))
return(updated_abstract)
abstract_processed = remove_punctuation(abstract_lemmatized)
ii. Removing stopwords
A fairly routine task in NLP is removing stop words, or common words that do not carry enough meaning to differentiate one text from another, e.g., ‘a’, ‘the’, ‘for’, and so on. I have used NLTK’s stopword library for this. It contains 179 words. As there are more words in a lifescience and biomedical research corpus such as ‘proof’,’record’,’researcher’, etc., that are not differentiating words, I added additional words (which I found in the current corpus) to the stopword list making it 520 words long. Additionally, in this step I lowercased all the letters, which is needed so as to avoid the algorithm reading ‘Read’ and ‘read’ as two different words.
def remove_stopwords(doc):
retracted_corpus=[]
for text in doc:
retracted_abstract=[]
for word in text:
word=word.lower()
if word not in nltk_stopwords:
retracted_abstract.append(word)
retracted_corpus.append(retracted_abstract)
return retracted_corpus
abstract_no_stop = remove_stopwords(abstract_processed)
iii. Making bigrams
Life sciences literature frequently containes bigrams such as ‘cell cycle’ and ‘protein phosphatase’. These bigrams convey a meaning that is not apparent when considering the either words individually. Therefore, I decided to collect bigrams using python library Gensim, another great python library for natural language processing. This step provides bigrams and unigrams where bigrams are selected according to specific conditions over the frequency of appearance in a corpus.
#using gensim to construct bigrams
from gensim.models.phrases import Phrases, Phraser
bi_phrases=Phrases(abstract_processed,min_count=5,threshold=10)
bigram = Phraser(bi_phrases)
#provides unigrams and bigrams
def dimers(doc):
updated_abstract=[]
for text in doc:
di = bigram[text]
updated_abstract.append(di)
return updated_abstract
abstract_bigram = dimers(abstract_no_stop)
After this I removed anything that is only numbers or is less than 2 characters long.
def abstract_bigram_clean(doc):
retracted_corpus=[]
for text in doc:
retracted_abstract=[]
for word in text:
if not word.isdigit() and len(word)>1:
retracted_abstract.append(word)
retracted_corpus.append(retracted_abstract)
return retracted_corpus
abstract_clean = abstract_bigram_clean(abstract_bigram)
From these processing steps, I obtained list of lists with each list containing words coming from a single abstract. To give an idea of the complexity of the corpus, there are 35,155 unique words in the corpus, which itself contains a little over 6,000 abstracts.
Building an LDA model
Before building a model, we need our corpus (all documents) to be present in a matrix representation. For this purpose, I prepared a dictionary where each unique word is assigned an index and then used it to make a document-term matrix also called bag-of-words (BoW). I have used Gensim for performing all these tasks. Additionally, there were 11,998 words that occur just once. I removed them as they do not indicate any pattern that the model will detect. Moreover, any word that occurs in more than 20% of the documents were removed as they seem to be not restrictive to a few topics.
# create a dictionary
from gensim.corpora import Dictionary
dictionary = Dictionary(abstract_clean)
dictionary.filter_extremes(no_below=2, no_above=0.2)
# convert the dictionary into the bag-of-words (BoW)/document term matrix
corpus = [dictionary.doc2bow(text) for text in abstract_clean]
To build an LDA model we need to provide the number of topics that we expect in the corpus. This can be tricky and needs multiple trial-and-error attempts as we do not know how many topics are present. One way to estimate this number is by computing coherence measure 2, a score that rates quality of topics computed by topic models and thus, differentiates a good topic model from a bad one.
Coherence measure is calculated in following four steps:
- Segmentation – in which word set $t$ can be segregated into word subsets $S$
- Probability calculation – where word probabilities $P$ are calculated based on the reference corpus
- Confirmation measure – both set of $S$ and $P$ are used by confirmation measure to calculate agreements $\phi$ of pairs of $S$
- Aggregation – Finally, all confirmations are aggregated to a single coherence value $c$.
In order to find the optimum number of topics in a corpus, one can build multiple LDA models with different number of topics. From these models one can choose the value of topics that has maximum score and ends the rapid growth of the coherence values. Increasing the number of topics further can lead to situations where many keywords are present in different topics. Gensim library provides an implementation of coherence measure.
# instantiating an lda model
LDA = gensim.models.ldamodel.LdaModel
#computing coherence for different LDA models containing different number of topics
def calculate_coherence(dictionary, corpus, texts, start, stop, step):
coherence_scores=[]
for num_topics in range(start,stop,step):
model=LDA(corpus=corpus, id2word=dictionary, num_topics=num_topics)
coherence_lda=CoherenceModel(model=model, texts=texts, dictionary=dictionary, coherence='c_v')
coherence=coherence_lda.get_coherence()
coherence_scores.append(coherence)
return coherence_scores
coherence_scores = calculate_coherence(dictionary=dictionary, corpus=corpus, texts=abstract_clean, start=2, stop=40, step=3)
We can observe multiple peaks, of almost the same heights, in the coherence values graph. The first peak comes at 14.
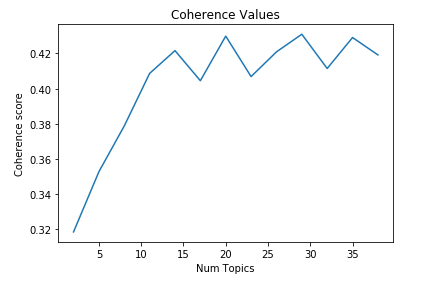
I decided to build my LDA model using 14 topics.
lda_model_abstract = LDA(corpus=corpus,id2word=dictionary, num_topics=14,
random_state=10,chunksize=6485,passes=100)
Visualization
This is a key step to read and understand the topics obtained from LDA and pyLDAvis helps us with that. pyLDAvis 3 is python package for interactive visualization of topics. It is derived from LDAvis which is a web based visualization tool for topics that are estimated using LDA.
pyLDAvis provides two panels for visualization: The left panel shows topics in the form of circles in two dimensions. The center of the circles is determined by calculating inter-topic distances and then using multidimensional scaling they are projected onto two-dimensions. Thus, topics that are closely related are closer. Additionally, the areas of circles represent overall prevalence of the topic. Thus, bigger the circle, more prevalent is the topic in the corpus. The right panel shows a bar chart of key terms for the selected topic on the left panel. The overlaid bars represent the topic-specific frequency of various terms in red color and corpus wide frequency in gray color. Thus, this right panel helps us find the meaning of the topics. Both the panels are linked in a way that selecting a topic in the left panel shows its important terms in the right panel. Additionally, on selecting a term on the right panel shows its conditional distribution in all the topics. An interesting thing in pyLDAvis is its method of ranking terms in a topic which is called relevance. Relevance is the weighted average of logarithm of a term’s probability and its lift. Lift is defined as ratio of the term’s probability in a topic to its marginal probability across the corpus. Relevance of a term $w$ to topic $k$ with weight parameter $λ$ can be mathematically defined as: $$ r(w,k| \lambda) = \lambda \log\phi_{k_w} + (1-λ) \log \frac{\phi_{k_w}}{p_w} $$ where $\phi_{k_w}$ is the probability of term $w \in 1..V$ for topic $k \in 1..K$ with $V$ being the number of terms in vocabulary of the corpus; $p_w$ is the marginal probability of term $w$ in the corpus. $\lambda$ lies between 0 and 1. It determines the weight given to the probability of term $w$ in the topic $k$ relative to the lift associated with $w$. When $\lambda=1$ then terms are ranked in decreasing order of their topic specific probability. When $\lambda=0$, terms are ranked in a topics according to their lift. pyLDAvis provides a user interface to adjust $\lambda$. For interpreting topics, I have kept $\lambda=0.6$, which is also the optimum value obtained from a user study 3.
You can check the visualization for the current analysis below.
Following topics were obtained (listed in decreasing order of their prevalence):
| No. | Topic | Key words | Remarks |
|---|---|---|---|
| 1. | Medical/Clinical | ‘clinical’, ‘diagnosis’, ‘symptom’, ‘lesion’ | |
| 2. | Cell cycle, cell proliferation, cell death | ‘apoptosis’, ‘akt’ (protein kinase b), ‘phosphorylation’, ‘cell cycle’ | |
| 3. | Cancer | ‘tumor’, ‘cancer’ , ‘metastasis’ , ‘invasion’, ‘breast cancer’ | |
| 4. | Oxidative stress | ‘oxidative stress’, ‘sod’ (superoxide dismutase), ‘resveratrol’, ‘ros’ | |
| 5. | Biophysics | ‘temperature’, ‘material’, ‘water’, ‘system’, ‘nanoparticle’ | |
| 6. | Immunology | ‘il’ (interlukin), ‘nf kappab’, ‘antigen’, ‘macrophage’, ‘immune’, ‘cytokine’, ‘antibody’ | |
| 7. | Medical/Clinical | ‘anesthesia’, ‘ponv’ (postoperative nausea and vomiting), ‘vommiting’ | Differ from topics 1 and 9 as it has terms related to anesthesia and nausea |
| 8. | Genetics and molecular biology | ‘domain’, ‘mutant’, ‘sequence’, ‘scaffold’, ‘stress’ | Related to genome, mutations and protein sequence |
| 9. | Medical/Clinical | ‘cholesterol’, ‘diabetes’, ‘insulin’ | Differ from topics 1 and 7 as it contain terms related to diabetes |
| 10. | Bone health | ‘bone’, ‘osteoporosis’ , ‘risedronate’ | |
| 11. | Gut and absorption | ‘intestinal’, ‘absorption’, ‘probiotic’ | It also contain terms that are related to topic 5 (a mixing which can be due to its proximity to topic 5) |
| 12. | Central nervous system and cognition | ‘brain’, ‘stimulus’, ‘visual’, ‘motor’, ‘bdnf’ | |
| 13. | Genetic polymorphism, database related | ‘polymorphism’, ‘genotype’, ‘pubmed’, ’embase’, ‘database’ | |
| 14. | Growth factors, hormones and body fluids | ‘csf’(cerebrospinal fluid), ‘scf’ (stem cell factor), ‘aba’ (abscisic acid) |
Conclusion:
Firstly, topic modeling using LDA showed a good resolution/separation of topic-specific terms for topics 1-9 and 12, except 5 and I found topic interpretation fairly easy. But the interpretation for other topics was difficult with many unrelated terms coming in a single topic, indicating that the topic model is picking up noise or idiosyncratic correlations in the corpus. Selecting more number of topics didn’t give any improvement in topic interpretation. Importantly, as the corpus is not big (only around 6000 articles), contains only abstracts (short text) and a vocabulary count of 23,157, these can be reasons why in some cases the topic model is picking noise.
Secondly, topics 1 to 7 showed similar topic prevalence that ranges from 10.2% to 7.9% of tokens. Thus, indicating most of these topics are equally important or prevalent in the corpus of retracted literature.
In conclusion, in spite of a small dataset, LDA could find 14 topics in the retracted literature which majorly include- Medical, Cell cycle and proliferation, Cancer, Immunology, Oxidative stress, Genetics, Central nervous system and cognition. It is not wrong to say that LDA is a very powerful tool that provides an easy and fast way to explore patterns or themes in the corpus.
The source code for this analysis can be found on my Github repository.
-
Blei, D.M., Ng, A.Y. and Jordan, M.I., 2003. Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), pp.993-1022. ↩
-
Röder, M., Both, A. and Hinneburg, A., 2015, February. Exploring the space of topic coherence measures. In Proceedings of the eighth ACM international conference on Web search and data mining (pp. 399-408). ACM. ↩
-
Sievert, C. and Shirley, K., 2014. LDAvis: A method for visualizing and interpreting topics. In Proceedings of the workshop on interactive language learning, visualization, and interfaces (pp. 63-70). ↩↩